힙

작성일 | 0 comments
181117 Today I learned heap

Heap

이진트리의 한 종류. 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리(Complete binary tree)를 기본으로 한 자료구조(tree-based structure)

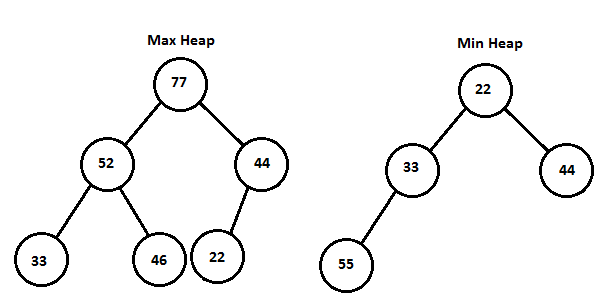
힙의 조건

  1. 루트 노드가 언제나 최댓 값(최대 힙) 또는 최솟 값(최소힙)을 가짐.
  2. 완전 이진 트리여야함. (leaf 노드 전의 level의 노드가 포화 이진트리여야함)
  3. 모든 노드에서 자신의 자식보다 큰 키(작은 키) 값을 가지고 있음.

http://3.bp.blogspot.com/-QGbIGtOsknY/VYxNnlUiIoI/AAAAAAAACCc/a06lp5qTcGo/s1600/Heap_Concept.png

힙 정렬

자료구조 힙을 사용해 시간복잡도 최대 O(nlogn)을 가지는 정렬 알고리즘

힙 정렬 과정

  1. 정렬되지 않은 리스트의 요소를 하나씩 힙에 insert 시간복잡도 O(logn)
  2. 모두 insert가 되면 하나씩 remove 하면서 새로운 리스트에 값을 insert 시간복잡도 O(logn)

이 과정을 거치면 정렬된 리스트를 반환한다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def heap_sort_desc(unsorted):
    """
    MAX 힙을 활용한 정렬 알고리즘
    힙 삽입의 시간 복잡도 O(logn)
    삭제의 시간 복잡도 O(logn)
    => O(nlogn) 복잡도
    :return:
    """
    h = MaxHeap()
    sorted = []

    for data in unsorted:
        h.insert(data)

    d = h.remove()
    while d:
        sorted.append(d)
        d = h.remove()

    return sorted